參考答案：A

　　參考解析：略

　　參考答案：A

　　參考解析：略

　　3.題目暫缺

　　參考答案：B

　　參考解析：略

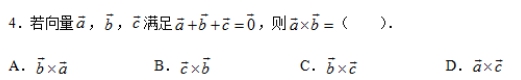
　　參考答案：C

　　參考解析：略

　　5.設n階方陣M的秩r(M)=r

　　A.任意一個行向量均可由其他r個行向量線性表示

　　B.任意r個行向量均可組成極大線性無關組

　　C.任意r個行向量均線性無關

　　D.必有r個行向量線性無關

　　參考答案：D

　　參考解析：略

　　6. 試題暫缺，參考答案C

　　7.下列對向量學習意義的描述:

　　①有助于學生體會數學與現實生活和其他學科的聯系;

　　②有助于理解數學運算的意義和價值，發展運算能力;

　　③有助于掌握處理，幾何問題的一種方法，體會數形結合思想;

　　④有助于理解數學不同內容之間存在廣泛的聯系.

　　其中正確的共有( ).

　　A.1條

　　B.2條

　　C.3條

　　D.4條

　　參考答案：D

　　參考解析：略

　　8.數學歸納法的推理方式屬于( ).

　　A.歸納推理

　　B.演繹推理

　　C.類比推理

　　D.合情推理

　　參考答案：B

　　參考解析：略

　　二、簡答題(本大題共5小題，每題7分，共35分)

　　參考解析：

　　(2)在該變換條件下，①不變的性質:都是中心對稱圖形和軸對稱圖形，都是在某條件下點的軌跡所形成的對稱圖形;②變化的性質:圖形形態發生了變化，不再以原點為中心點，不再與x軸和y軸相交，圖形距離中心點的距離都相等。

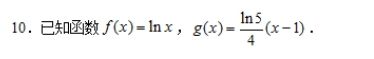
　　(1)求f(x)和g(x)圍成的平面區域的面積.

　　(2)求0≤y≤f(x), 1≤x≤3,繞y軸旋轉的體積.

　　查看答案

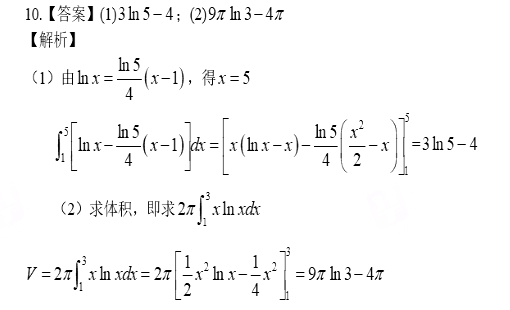
　　11.一個袋子里有8個黑球，8個白球，隨機不放回連續取球5次，每次取出1個球，求最多取到3個白球的概率.

　　參考解析：

　　12.給出數學文化的內容，請舉出數學課堂中兩個能夠應用數學文化的例子.

　　參考解析：

　　數學是一門與概念、定理、公式相關的學科，教師在數學教學中滲透數學文化、設置與教學內容相關的且蘊含在現實生活中的數學文化、引導學生思考其中所隱含的數學知識和規律，對學生的數學學習具有巨大的幫助。例如:

　　(1)在學習《整數和負數》時，“負數” 概念對學生來說相對抽象。教師可以在教學中滲透數學文化史:中國是最早提出負數的國家，《九章算術》 是最早、最完整介紹負數的古書，人們在求解方程時經常會遇到小數減大數的情形，為便于求解，便創造了負數;在古代為區分正負數，數學家創造了一種方法:用不同顏色的算籌來表示正、負數;中國古代不僅提出了負數的概念，還提出了整套的正、負數的運算法則，這些法則沿用至今。教師在教學中融入數學文化，讓學生了解概念產生的背景和意義，利用概念與生活的相通性可以幫助學生更直觀地理解概念。

　　(2)在教學《勾股定理》時，可以從畢達哥拉斯到朋友家做客的故事入手:畢達哥拉斯是古希臘最為著名的數學家之-，相傳2500年前，他到朋友家做客，發現朋友家用地板磚鋪成的地面反映出了直角三角形的三邊關系。畢達哥拉斯發現直角三角形的三邊關系的故事為《勾股定理》的教學提供了問題引入，學生通過思考故事中隱含的規律，從而進行猜想假設，再加上教師的演示將定理變得具體形象，學生能夠更容易地總結出直角三角形的三邊關系，即勾股定理。探究勾股定理相關的數學文化史的過程蘊含了豐富的數學思想方法，這對學生理解定理極為有利。

　　將數學文化滲透到數學教學中,將教材內容與數學文化巧妙結合起來，從數學文化中延伸出數學概念和規律，可以幫助學生理解相關內容。數學文化中蘊含的故事具有較強的趣味性，還可以激發學生的學習興趣。

　　13.簡述數學建模的主要過程.

　　參考解析：

　　數學建模是運用數學思想、方法和知識解決實際問題的過程。建立和求解模型的過程包括:從現實生活或具體情境中抽象出數學問題，用數學符號建立方程、不等式、函數等表示數學問題中的數量關系和變化規律，求出結果、并討論結果的意義。具體如下:

　　(1)模型準備:了解問題的實際背景，明確其實際意義，掌握對象的各種信息。以數學思想來包容問題的精髓，數學思路貫穿問題的全過程，進而用數學語言來描述問題。要求符合數學理論，符合數學習慣，清晰準確。

　　(2)模型假設:根據實際對象的特征和建模的目的，對問題進行必要的簡化，并用精確的語言提出一-些恰當的假設。

　　(3)模型建立:在假設的基礎上，利用適當的數學具來刻劃各變量常量之間的數學關系，建立相應的數學結構(盡量用簡單的數學工具)。

　　(4)模型求解:利用獲取的數據資料，對模型的所有參數做出計算(或近似計算)。

　　(5)模型分析:對所要建立模型的思路進行闡述，對所得的結果進行數學上的分析。

　　(6)模型檢驗:將模型分析結果與實際情形進行比較，以此來驗證模型的準確性、合理性和適用性。如果模型與實際較吻合，則要對計算結果給出其實際含義，并進行解釋。如果模型與實際吻合較差，則應該修改假設，再次重復建模過程。

　　三、解答題(本大題1題, 10分)

　　14.已知函數f(x)在閉區間[a,b].上連續，且f(a).f(b)<0,請用二分法證明f(x)在(a,b)內至少有一個零點。

　　參考解析：

　　證明過程見解析。

　　四、論述題(本大題1小題，15分)

　　15.有人認為目前的教學缺乏對中學生思維能力的培養，請談一談你的看法，并說一說在老師在教學中應該如何做。

　　參考解析：

　　現代教育觀點認為，數學教學活動是數學活動的教學，即思維活動的教學。孔子說: “學而不思則罔，思而不學則殆”,養成良好的思維品質是教學改革中的一個重要課題，在數學學習中要使學生思維活躍，就要教會學生分析問題的基本方法，在如今的教育體制之下灌輸式教學還是很常見，從而忽視了對學生學習思維的培養，這對于學生創新能力的培養是極其不利的，因此在教育體制改革的趨勢之下，我們不僅要重視學生基本知識和基本技能的學習，更應該注重學生思維品質的培養。心理學家認為，培養學生的數學思維品質是培養和發展數學能力的突破口。思維品質包括思維的深刻性、敏捷性、靈活性、批判性和創造性，它們反映了思維的不同方面的特征，因此在教學過程中應該有不同的培養手段。

　　思維的深刻性既是數學的性質決定了數學教學既要以學生為基礎，又要培養學生的思維深刻性。數學思維的深刻性品質的差異集中體現了學生數學能力的差異，教學中培養學生數學思維的深刻性，實際上就是培養學生的數學能力。數學教學中應當教育學生學會透過現象看本質，學會全面地思考問題，養成追根究底的習慣。

　　數學思維的敏捷性主要反映了正確前提下的速度問題。因此，數學教學中，一方面可以考慮訓練學生的運算速度，另一方面要盡量使學生掌握數學概念、原理的本質，提高所掌握的數學知識的抽象程度。因為所掌握的知識越本質、抽象程度越高，其適應的范圍就越廣泛，

　　五、案例分析題(本大題1題, 20分)

　　16.在學習了“直線與圓的位置關系”后，一位教師讓學生解決如下問題:

　　參考解析：

　　(1) 該同學的解法沒有考慮直線L斜率不存在的情況，沒有掌握數學當中分類討論的思想和斜率的定義。正確解法①如上同學做題步驟，且過論當斜率不存在時，直線L方程為x=2符合題意;②第二種做法可以先求出切點坐標，然后再求方程，易知切點為

　　檢索的速度也就越快。另外，運算速度不僅僅是對數學知識理解程度的差異，而且還有運算習慣以及思維概括能力的差異。因此，數學教學中，應當時刻向學生提出速度方面的要求，使學生掌握速算的要領。

　　為了 培養學生的思維靈活性，應當增強數學教學的變化性，為學生提供思維的廣泛聯想空間，使學生在面臨問題時能夠從多種角度進行考慮，并迅速地建立起自己的思路，真正做到舉一反三”。教學實踐表明，變式教學對于培養學生思維的靈活性有很大作用。

　　六、教學設計題(本大題1小題，30分)

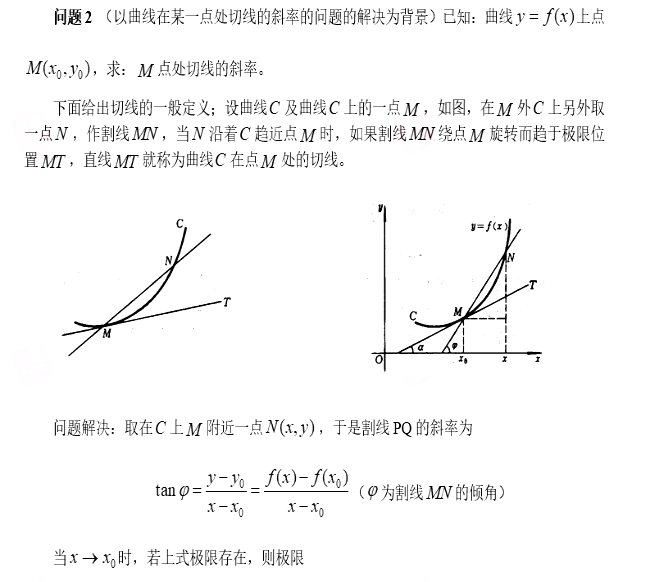
　　17.普通高中課程標準2017版，對“導數的概念及其意義”提出的學習要求為:

　　①通過實例分析,經歷由平均變化率過渡到瞬時變化率的過程，了解導數概念的實際背景,知道導數是關于瞬時變化率的數學表達，體會導數的內涵與思想。

　　②體會極限思想。

　　③通過函數圖象直觀理解導數的幾何意義。

　　針對導數的概念及其意義以達到①，完成教學設計。

　　(1)設計教學重點(6分)。

　　(2)教學過程(導入、概念形成與鞏固)，并寫出設計意圖(24分)。

　　參考解析：

　　(1)教學重點:深刻理解在一點處導數的概念，能準確表達其定義;注意

　　[設計意圖]教學中遵循“學生為主體,教師為主導，訓練為主線，發展思維為主旨”的“四主原則”。以恰當的系列活動為紐帶，給學生創設自主探究、合作交流的時間與空間，引導學生經歷數學知識再發現的過程，讓學生在參與中獲取知識，發展思維，感悟數學。

　　③鞏固概念:利用導數定義求是數的幾個例子

　　[設計意圖]加深學生對導數內涵的理解，熟練應用導數的概念進行運算，提煉求導步驟由特殊到一般，完成思維的飛躍。通過具體例題的分析，加深學生對導數內涵的理解，體驗數學在實際生活中的應用。